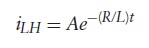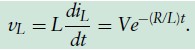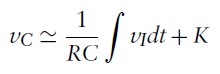10.4 Propagation Delay and the Digital Abstraction

• Example inverters connect in series:

• Characteristic of ideal and actual inverters:

• tpd,1-0 is the propagation delay through inverter A for a 1 to 0 transition
• tpd,0-1 is the propagation delay through inverter A for a 0 to 1 transition
• tpd,1-0 and tpd,0-1 delays are not necessarily equal
• For simplicity, we characterize digital gates by a single delay, propagation delay tpd:

10.3 Intuitive Analysis

• Linear RC circuits has two basic form of solution:
• Rising transient

• Failing transient

• For liner RL circuits, time constant is L/R
• For simple excitations (step and impulse), the response of first-order systems can be sketched with some intuition.
• Example:

 

• The form of response - vC(t) can be sketched intuitively by identifying three intervals of operation:
• Initial interval 
• Transition interval
• Final interval
• Completer response:

10.2 Analysis of RL Circuits

• Inductor current buildup:

• By KVL:

• Homogeneous equation:

• Homogeneous solution (time constant = L/R):

• Particular equation: 

• Particular solution:

• Complete solution:

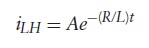
• Initial & continuity conditions are applied to evaluated A
• Inductor current for t > 0 :

• Inductor voltage :

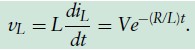
• Inductor current has an initial value of 0 (open circuit) and final value of V/R (short circuit)

10.1.4 Series RC Circuit, Square Wave Input

• When a square pulse is applied to the RC circuit, a decidedly non-square pulse, with slow rise and slow decay, results.
• The capacitor has allowed us to do a limited amount of wave shaping.

• Response to square wave:

• b: Short time constant compare to square-wave period
• c: Time constant is a substantial fraction of the pulse length
• d: Time constant is longer than square-wave period (transient does not go to completion)

• For large RC, the capacitor voltage is approximately the integral of the input voltage (useful signal-processing property)

10.1.3 Series RC Circuit, Step Input

10.1.2 RC Discharge Transient

• RC discharge transient:

• Properties of exponentials: aid to sketching waveform for decaying exponential in simple RC & RL transients

10.1.1 Parallel RC Circuit, Step Input

• Capacitor charging transient

• To find vc(t), we must solve a non-homogeneous, linear first-order ordinary differential equation with constant coefficients: 

• To solve this equation, we will use the method of homogeneous and particular solutions because this method can be readily extended to higher order equations

• The method states that the solution to the non-homogeneous differential equation can be obtained by summing together the homogeneous solution and the particular solution

• Total solution (vCH(t) is called the homogeneous solution and vCP(t) is called the particular solution)

• When dealing with circuit responses, the homogeneous solution is also called the natural response of the circuit because it depends only on the internal energy storage properties of the circuit and not on external inputs. The particular solution is also called the forced response or the forced solution because it depends on the external inputs to the circuit.

• The root of the characteristic equation, s, is also called the natural frequency of the system.

• Complete solution: