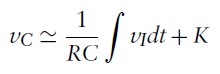10.7.4 A Static Memory Element

• The static memory element can store a value written into it indefinitely 
• Static memory element example using a trickle switch:

10.7.3 Design of the Digital Memory Element

• Circuit implementation of a memory element:

10.7.2 An Abstract Digital Memory Element

• An abstract one-bit memory element:

10.7 Digital Memory

10.7.1 The Concept of Digital State

• The value stored in memory is simply a digital state variable in a manner analogous to an analog state variable value stored on a capacitor

10.5.3 Zero-Input and Zero-State Response

• State variable allows us to solve transient problem by superposition
• Total response is the sum of the zero-input-response (ZIR) and the zero-state-response (ZSR)
• The particular solution and the homogeneous solution are terms which apply to a method of solving differential equations 
• Zero-input and zero-state responses arise from a particular way of partitioning the circuit problem into two simpler subproblems. The resulting subcircuits can be solved by finding the homogeneous solution and particular solution in each case.

10.5.2 Computer Analysis using the State Equation

• One advantage of state equation formulation is that even in the nonlinear case, the equations can be readily solved on a computer
• The value of state variable at time t + dt can be estimated by standard numerical method ie. Euler's method:

• The value of vC at time t = t + 2dt can be determined in like manner from the value of vC(t0+dt) and i(t0+dt) . Subsequent value of vC can be determined in same process
• By choosing small value of dt, a computer can determine the waveform of vC(t) to a certain degree of accuracy
• This process illustrates the fact that the initial state contains all the information that is necessary to determine the entire future behavior of the system from the initial state and subsequent input
• This procedure works even for circuits with many capacitors and inductors, linear or nonlinear, because these higher-order circuits can be formulated in term of a set of first order state equations, one for each energy storage element ( with an independent state variable) in the network

     

10.5 State and State Variables

10.5.1 Concept of State

• Analysis of capacitor and inductor circuits based on their state/memory aspect is used when the circuit is non-linear or contains a large number of storage elements
• Voltage as a state variable:

• All of the relevant past history of the circuit prior to t1 is summarized in one value, q(t1)
• Variables that have this property are called state variables
• If we know the value of state variable at one time, and the value of input variable thereafter, we can find the value of the state variable for any subsequent time
• The first order differential equations for RC and RL circuits can be written as:

• Linear case:

10.4 Propagation Delay and the Digital Abstraction

• Example inverters connect in series:

• Characteristic of ideal and actual inverters:

• tpd,1-0 is the propagation delay through inverter A for a 1 to 0 transition
• tpd,0-1 is the propagation delay through inverter A for a 0 to 1 transition
• tpd,1-0 and tpd,0-1 delays are not necessarily equal
• For simplicity, we characterize digital gates by a single delay, propagation delay tpd:

10.3 Intuitive Analysis

• Linear RC circuits has two basic form of solution:
• Rising transient

• Failing transient

• For liner RL circuits, time constant is L/R
• For simple excitations (step and impulse), the response of first-order systems can be sketched with some intuition.
• Example:

 

• The form of response - vC(t) can be sketched intuitively by identifying three intervals of operation:
• Initial interval 
• Transition interval
• Final interval
• Completer response:

10.2 Analysis of RL Circuits

• Inductor current buildup:

• By KVL:

• Homogeneous equation:

• Homogeneous solution (time constant = L/R):

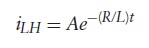
• Particular equation: 

• Particular solution:

• Complete solution:

• Initial & continuity conditions are applied to evaluated A
• Inductor current for t > 0 :

• Inductor voltage :

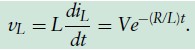
• Inductor current has an initial value of 0 (open circuit) and final value of V/R (short circuit)

10.1.4 Series RC Circuit, Square Wave Input

• When a square pulse is applied to the RC circuit, a decidedly non-square pulse, with slow rise and slow decay, results.
• The capacitor has allowed us to do a limited amount of wave shaping.

• Response to square wave:

• b: Short time constant compare to square-wave period
• c: Time constant is a substantial fraction of the pulse length
• d: Time constant is longer than square-wave period (transient does not go to completion)

• For large RC, the capacitor voltage is approximately the integral of the input voltage (useful signal-processing property)

10.1.3 Series RC Circuit, Step Input

10.1.2 RC Discharge Transient

• RC discharge transient:

• Properties of exponentials: aid to sketching waveform for decaying exponential in simple RC & RL transients

10.1.1 Parallel RC Circuit, Step Input

• Capacitor charging transient

• To find vc(t), we must solve a non-homogeneous, linear first-order ordinary differential equation with constant coefficients: 

• To solve this equation, we will use the method of homogeneous and particular solutions because this method can be readily extended to higher order equations

• The method states that the solution to the non-homogeneous differential equation can be obtained by summing together the homogeneous solution and the particular solution

• Total solution (vCH(t) is called the homogeneous solution and vCP(t) is called the particular solution)

• When dealing with circuit responses, the homogeneous solution is also called the natural response of the circuit because it depends only on the internal energy storage properties of the circuit and not on external inputs. The particular solution is also called the forced response or the forced solution because it depends on the external inputs to the circuit.

• The root of the characteristic equation, s, is also called the natural frequency of the system.

• Complete solution:

Chapter 10 First-Order Transients in Linear Electrical Networks

• Systems with one storage element (capacitor/inductor) are described by first-order differential equations

9.5 Energy, Charge and Flux Conservation

• Circuit analysis with initial charge/flux linkage (switch closed at t = 0s):

• Energy is lost when v1 is not equal to v2:

Inductors Series and Parallel Connection

• Series Connection:

• Parallel Connection:

9.2.1 Capacitors Series and Parallel Connections

• Series connection:

• Parallel connection:

9.1.2 Inductors

• Idealized toroidal inductor ( u = magnetic permeability)

• Magnetic flux density, B

• Magnetic flux density across the core

• Total magnetic flux linkage (Weber/Wb)

• Inductance (Webers/Ampere, Henry)

• For linear time-invariant inductor:

• Inductor memory property:

• Inductor energy property: